Reale Automaten🔖

Allgemein Abstraktion eines realen Automaten🔖

Soll unabhängig von einer Implementierung der Automat modelliert werden, so benötigt man folgende Bestandteile:

1. Eingabemedium

z.B. ein Band bestimmter Länge, das die Eingaben einzeln (feldweise) enthält

2. Ausgabemedium

z.B. ein geschlossenes Band, dass die Ausgabeelemente feldweise erfasst

3. Zentraleinheit

zur Steuerung des Automaten und zur Speicherung der inneren Zustände

4. Lesekopf

zum Lesen des Eingabebandes

5. Schreibkopf

zum Schreiben auf das Ausgabeband

Definition Mealy-Automat – Transduktor🔖

Die Elemente von X nennt man Eingabezeichen, die von Y Ausgangszeichen, die von Z Zustände. Y* ist die Menge aller endlichen Folgen aus Y einschließlich des leeren Wortes. Die Angabe der Überführungs- und Ausgabefunktion erfolgt üblicherweise in Tabellen oder mit Hilfe des Zustandsdiagramms.

Reale Automaten	Definition Endlicher Automat
Reale Automaten finden sich z. B. in Form von Geldautomaten, Parkscheinautomaten, Getränkeautomaten, usw..	Die Erkenntnisse aus den realen Automaten sollen in einem informatischen Modell standardisiert vereinbart werden (als allgemeine Abstraktion eines realen Automaten), da dieses Modell das typische informatische EVA-Prinzip wiedergeben kann.
Analysiert man reale Automaten so stellt man fest realer Automat hat	Der endlicher Automat mit Ausgabe (Transduktor, Mealy-Automat) lässt sich aus der Verall­ge­mei­ne­rung der Analyse realer Automaten ableiten besitzt:
- Eine Menge an möglichen Eingaben in den Automaten: z.B.: Geldstücke mit bestimmter Wertigkeit, Tastendruck o. ä.	- Eine nichtleere, endliche Menge – das Eingabealphabet (genannt E)
- Eine Menge an mögliche Ausgaben des Automaten: z.B.: Getränke, Fahrkarten, Rückgeld usw.	- Eine nichtleere, endliche Menge – das Ausgabealphabet (genannt A)
- Zustände, die im Laufe seiner Arbeit durchlaufen werden z.B.: Schranke ist unten, 10 Cent eingeworfen, 20 Cent eingeworfen, ...	- Eine nichtleere, endliche Menge – die Zustandsmenge (genannt Z)
- einen Startzustand z.B.: bereit zur Eingabe	- z0 --> Z ist der Anfangszustand
- Endzustände z.B.: Geldausgabe, Getränkeausgabe, Störung ...	- Ausgezeichnete Zustände, die Endzustände
- Funktionen, die Übergänge zwischen den Zuständen und die Ausgabe regeln. z.B.: Wird noch 1 EUR eingeworfen, so gib 50 Cent aus und wechsele in den Zustand „Schranke oben"	- u: E × Z --> Z ist die Überführungsfunktion, welche jedem Paar (Eingabezeichen, Zustand) einen Folgezustand zuordnet - g: A × Z --> Y ist die Ausgabefunktion, welche jedem Paar (Eingabezeichen, Zustand) eine Ausgabe zuordnet.

1.1 Darstellung eines Automaten als Graph

Versucht man diese Übergangsfunktion grafisch darzustellen, erhält man einen Zustandsgraphen bzw. ein Zustandsdiagramm. Ein solcher Graph besitzt folgende stehende Elemente.

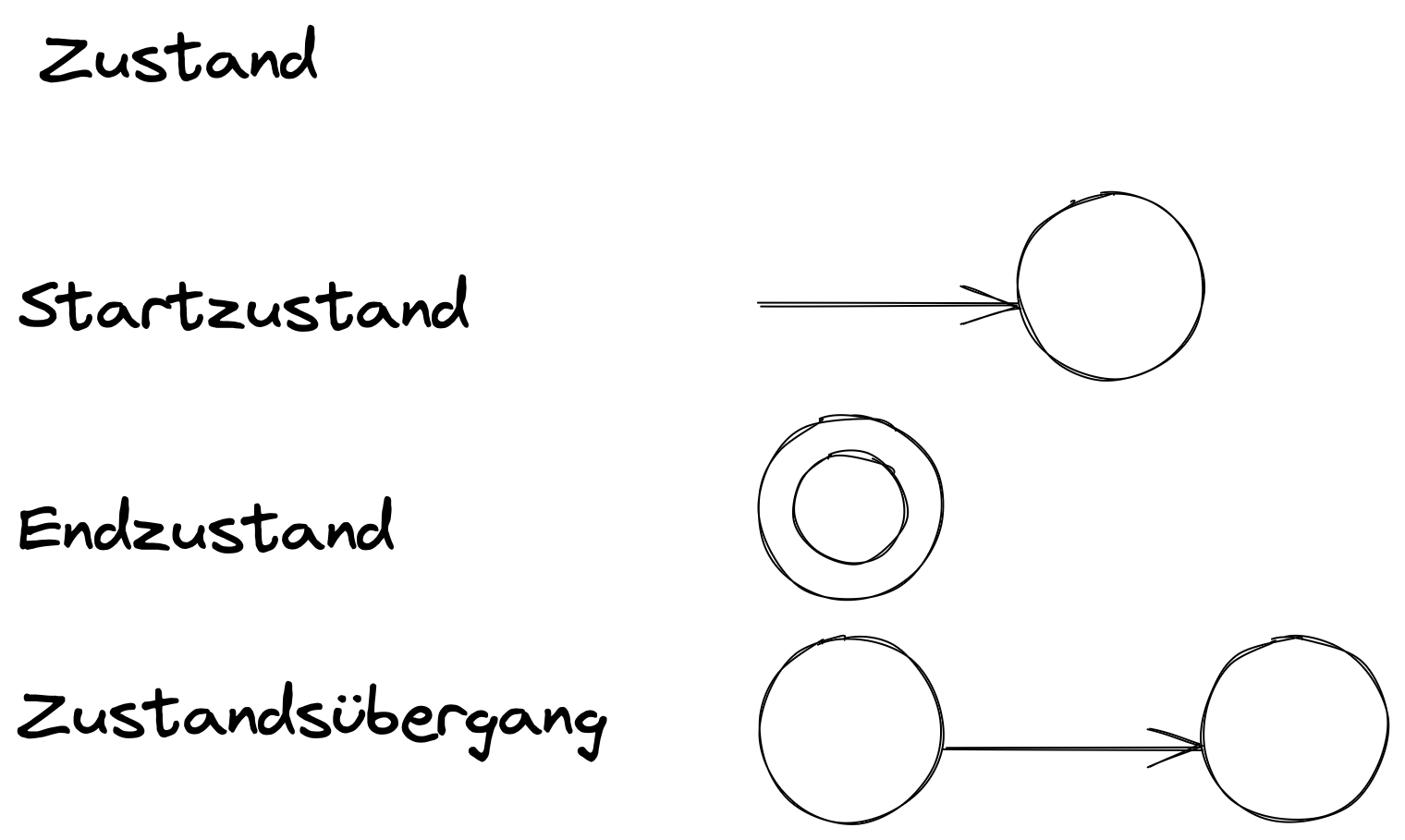
Ein Beispiel – Parkscheinautomat🔖

Auf einem Parkplatz kostet das Parken ohne Zeitbegrenzung 2,00 €. Nach Einwurf der korrekten Geldsumme (0,50€, 1,00 € und 2,00 €) soll sich eine Schranke zeit- und lichtsensorgesteuert öffnen/schließen. Der Automat wechselt nicht, gibt zu viel gezahltes Geld nicht zurück und hat keine Möglichkeit des Abbruchs.

Analyse: Der Parkscheinautomat hat

|eine Menge von Eingabeobjekten | Geldstücke mit Wertigkeiten 0,5 €, 1 € und 2 €. | E= { 0,5 | 1 | 2} | |--- |--- |--- | |eine Menge von Ausgabeobjekten | Schranke öffnen, nichts (wenn z. B. zu wenig Geld eingeworfen wurde) |A = { „Schranke öffnen“ } | |Zustände |{„kein Geld“, „50 Cent“, „1 EUR“, „1,50 EUR“ |Z = { 0 | 0,50 | 1,00| 1,50 } | |einen Startzustand |bereit zur Eingabe |Z = {0} | |Endzustände |Schranke öffnen || |Funktionen, die die Zustandsübergänge und die Ausgabe regeln.| Graphische Darstellung (siehe unten)||

1.2 Darstellung von Automaten mit Hilfe von Tabellen

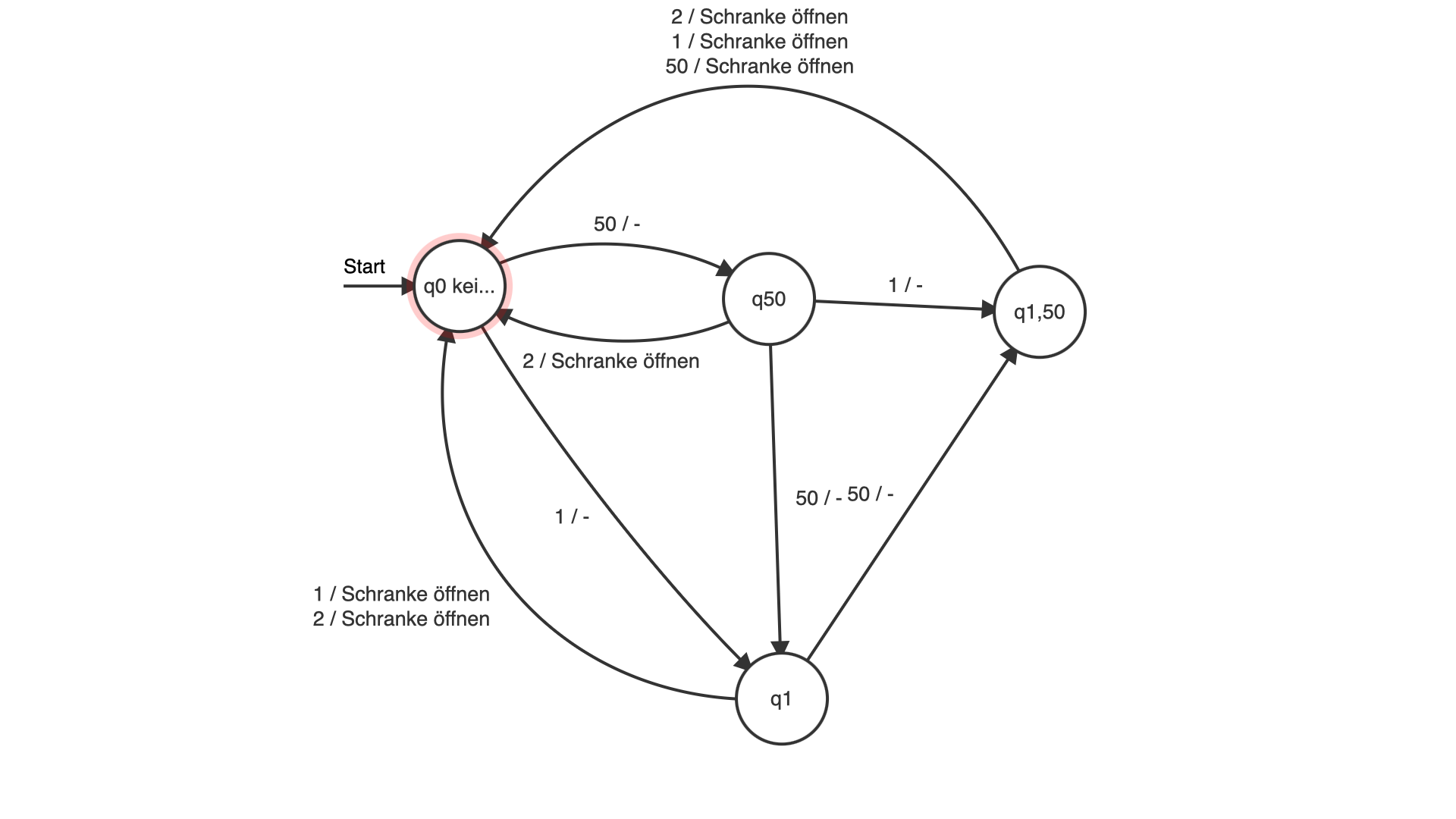
• Darstellung der Überführungsfunktion u: X × Z --> Z | u | z0 | z50 |z100 |z150 | | --- | --- | --- | --- | --- | |E50 |z50 |z100 |z150 |z0 | |E100 |z100 |z150 |z0 |z0 | |E200 |z0 |z0 |z0 |z0 |

• Ausgabefunktion g: X × Z --> Y* | g | z0 | z50 | z100 |z150| | --- | --- | --- | --- | --- | | E50 | yn | yn | yn | ys| | E100 | yn | yn | ys | ys| | E200 | ys | ys | ys | ys|

Die Darstellung in Form einer Tabelle in der der neue Zustand getrennt von einem Semikolon die Ausgabereaktion notiert wird ist ebenfalls gebräuchlich.

u	z0	z50	z100	z150
x50	z50;yn	z100;yn	z150;yn	z0;ys
x100	z100;yn	z150;yn	z0;ys	z0;ys
x200	z0;ys	z0;ys	z0;ys	z0;ys

Zustandsübergangsfunktion

Die für den Automaten wichtige Frage lautet etwa:

Wie ändert sich sein Zustand beim Betätigen einer Taste bzw. beim Einwurf einer Münze?

Da hierzu sowohl der aktuelle Zustand als auch die Eingabeaktion des Benutzers als Vorgaben nötig sind, werden einem Elementepaar (s;e) mit s \in S und e \in E ein neuer Folgezustand zugeordnet. Da der jeweilige Folgezustand s' \in S eindeutig sein muss, liegt mathematisch gesehen eine Funktion vor, die so genannte Zustandsübergangsfunktion: (s;e)--> s'.

Zwei Eingangselementen wird demnach ein Ergebniselement zugeordnet, ähnlich etwa der Multiplikation, bei der zwei Zahlen ein Ergebnis zugeordnet wird. Eine übersichtliche Darstellung von Produkten bestimmter Zahlkombinationen erfolgt üblicherweise in einer Multiplikationstafel, die zweidimensional ist.

Dabei werden die möglichen Elemente der ersten Menge in der Eingangsspalte der Tabelle notiert, die der zweiten Menge in der Eingangszeile. Die zugeordneten Elemente stehen an den zugehörigen Kreuzungsstellen im Innenbereich der Tabelle.

Ausgabefunktion Für den Anwender interessanter sind allerdings die Ausgaben des Automaten. Auch diese hängen sowohl vom aktuellen Zustand als auch von der erfolgten Eingabe ab. Daher liegt auch hier eine Funktion im oben beschriebenen Sinne vor, die so genannte Ausgabefunktion: (s;e) --> a mit a \in.